Key Changes
Jump to: Changing to G, C, F, B flat, E flat | Changing to D, A, E, and B | Why Notation Changes
Legend
Left Column: Musical Key
Top: Note, scientific notation
Bottom: String number
Center: Notation
D, G, C, F, B flat, E flat - Shift Bridges to the Right
There are several keys that can be reached from D by shifting bridges to the right.
Starting with key of D: (D,E,F#,A,B)
Change to key of G by moving F# bridges to the right until they play G.
(Bridges #4, #9, #14, #19)
Starting with key of G (G,A,B,D,E):
Change to key of C by moving B bridges to the right until they play C.
(Bridges #2, #7, #12, #17)
Starting with key of C (C,D,E,G,A)
Change to key of F by moving E bridges to the right until they play F.
(Bridges #5, #10, #15, #20)
Starting with key of F (F,G,A,C,D)
Change to key of B♭ by moving A bridges to the right until they play B♭.
(Bridges #3, #8, #13, #18)
Starting with key of B♭ (B♭,C,D,F,G)
Change to key of C by moving D bridges to the right until they play E♭.
(Bridges #1, #6, #11, #16, #21)
Ending on key of E♭: (E♭,F,G,B♭,C)
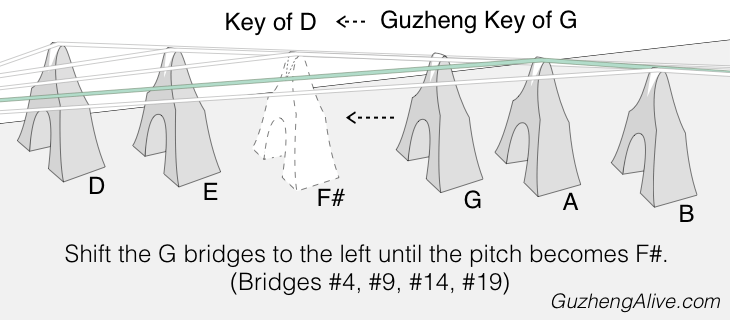
D, A, E, and B - Shift Bridges to the Left
There are several keys that can be reached from G by shifting bridges to the left.
Starting with key of G: (G,A,B,D,E)
Change to key of D by moving G bridges to the left until they play F#.
(Bridges #4, #9, #14, #19)
Starting With key of D: (D,E,F#,A,B)
Change to key of A by moving D bridges to the left until they play C#.
(Bridges #1, #6, #11, #16, #21)
Starting with key of A: (A,B,C#,E,F#)
Change to key of E by moving A bridges to the left until they play G#.
(Bridges #3, #8, #13, #18)
Starting with key of E: (E,F#,G#,B,C#)
Change to key of B: by moving E bridges to the left until they play D#.
(Bridges #5, #10, #15, #20)
End on key of B: (B,C#,D#,F#,G#)
Tuning Example
The Key of D has the notes D,E,F#,A,B. The 1st scale degree or tonic note is D. So, sheet music is written as 1,2,3,5,6 where D=1. The Key of G shifts each F# bridge slightly to the right to become G. You end up with the notes D,E,G,A,B, BUT we change the notation to start counting with G =1. So on sheet music, 1,2,3,5,6 means G,A,B,D,E.
Confusing, right? Well, there's one helpful principle: If your instrument's bridges are placed correctly you'll notice alternating sets of 3 and 2. The left bridge in the set of 3 is always number 1 on sheet music. This holds for all of the following 9 keys.
Why?
So why does the notation change with each key? In part that’s because of music theory - we number the strings based on their “scale degree”, or relative place in a 7-note scale. In practice it helps players know how far they need to press strings to get to the next note in the key. By shifting which note is “1” we guarantee that the “4” note is always a half step above “3” and the “7” note is always a whole step above “6”. The 3 string only needs to be pressed a little bit to reach the 4 but the 6 needs a larger press to reach 7. If the notation did not change the player could not predict how far to press strings.
Fun note:
According to Kwok 1987, determining the tuning an instrument is in by listening to a song is so difficult as to be impossible. Most songs use a combination of open and pressed strings to cover a range of as much as 4 notes on a single string. A musician could play the same set of notes on several different turnings depending on how much and how many strings they pressed.
To see more about guzheng tuning and how different keys play out across the entire instrument, visit the Tuning page.